堅さは手で触れれば分かるが、見た目では分からない。白い色は視感から認識できるが、触感からは判断できない。硬さと色は独立で別な概念であるから、これらを同じ土俵の上にのせること――堅さと白さが同じか、どれくらい異なっているかを議論すること――は意味がない。そのため、堅白同異(けんぱくどうい)は矛盾することを無理にこじつけることの譬である。堅と白は比較できないが、堅と堅あるいは白と白は比較できる。では、比較とは、人はどのように考え、どのような規則を使って、言葉にするのだろうか?
比較の論理構造をじっくり考えたことがある人は多くはないかもしれないが、実は、日常の会話の奥底には、厳密な比較の数学原理が潜んでいる。本稿の目的は、比較の言語表現をベクトルの内積、さらに一般的に「写像」の概念を使って定式化することにある。そう言うと、ある読者はこう言うかもしれない。比較表現を数学的に解析したからといって、それは数学的ペダンティック以上の意味はなく、理系人間の自己満足でしかない。しかし、ここで必要な数学は高等学校で習う程度である。否、論点はこれではない。この研究を進めると、比較の言い回しがニュートン力学、量子力学、確率過程論(ブラウン運動、ノイズなどのランダム現象)と同じ基盤の上に立っていることを理解できるのである。二十億光年の広闊(こうかつ)たる孤独な宇宙空間における自然現象の科学的エッセンスがちっぽけな人間の言葉の襞にも漉き込まれているという空想が湧いてくる。だからどうしたなぞとは言わないで、私の話にお付き合い頂ければ幸いである。
もっとも単純な例から比較の数学原理を考えよう。小石の重さの比較は、二つの小石の重さを秤ではかり、そのグラム数を記録すれば行える。これは説明する必要もないほど単純であるが、次の三つの成分(比較の三成分)から成り立っている。
● 要素(個体、対象)
● 尺度またはスケール(測定値)
● 関係または判定基準(>、<、=)
先ず、比較の対象をすべて――最少二個――を集めて集合を作る。この集合の要素(または元)が比較の対象であり、これらは番号または名称で一つ一つ識別する。測定値はある決まった尺度から求まる量であり、ここでは、同じ秤ではかった小石の重量である。判定基準はどちらが重いかまたは軽いかという判定のもととなるルールである。重さ(尺度)は一つ一つの対象に関する特徴であるが、どちらかを選ぶ判定基準は二つの対象の間に成り立つ関係である。この違いがあるからこそ、三成分すべてが比較には不可欠である。この三成分は数学の集合論(順序集合)とプログラム言語(C++)の基礎概念である[1]。
参考のために、比較(判断)に関する鈴木大拙の言葉を紹介する。「知恵とはどんな意味か、これは判断ということの意味である。判断というのは、甲のものと乙のものを対照して、そしてその間に一つの判定を下すということである。」[2]。
本稿では、英語の文から比較の原理を考察する。形容詞の比較級を用いる英語の表現では、日本語訳からは想像し難い事柄が比較されていたりする。たとえば、「彼は頭が良いというより賢い」とか「生きた心地がしなかった」である(以下参照)。他の例としては、クジラの公式「クジラが魚でないのは、馬が魚でないのと同じである」がある[1]。日本語からは、これらは比較というよりも二者択一と捉えられるかもしれないし、その比較級の使い方はそれこそ堅白同異と感じられるかもしれない。しかし、二者択一は比較の結果であるから、その根底には比較――鈴木大拙の「知恵」――があり、言うまでもなく、その英語の表現は正論である。つまり、日本語から出発すると、比較表現の機微を見逃すことが往々にしてあり、比較論理の多様性と統一性を的確に把握することが難しい。そこで、本稿では英語の文を取りあげて議論を進める。多くの英語の表現は、日本語訳からは察し難くても、比較の三成分に厳密に従っている。ここに、比較の論理の構造的な明晰さと奥深さがある。先ずは、日常の言葉の裏に潜んでいる比較の三成分を一つ一つ検証して行こう。
最初に、最も単純な例を挙げる。
The hailstones were bigger than golf balls.―その雹の粒はゴルフボールより大きかった。
比較の対象はhailstones(H)とgolf balls(G)、尺度はbigger、判定基準はthanである――biggerとthanを合わせて尺度と判定基準であるとしても良い。例文には、HとGの評価に数値が与えられていないが、球体の直径(または体積)という尺度ではかったHとGの値――たとえ目視であっても――が無ければ、比較はできない。暗黙にではあるが、話し手はHにGより大きな測定値を与えている。すると、H>Gの関係が成り立ち、比較が成立する。この例文は小石の比較とまったく同じ論理、つまり比較の三成分に基づいた論理形式であることが分かる。
次の例は本稿の主題である。最初の例はスケールが一つ(bigger)であるが、こちらでは複数のスケールが考慮されている。
He is more wise than clever. ―彼は頭が良いというより賢い。
この文を解析すれば、対象は「He is wise.」と「He is clever.」、関係はthan、スケールがmoreであることが分かる。この比較では、先ず彼の頭の良さを測り、次に彼の賢さを測り、これらの測定値をmoreスケールで比べている。賢さと頭の良さのスケールは独立である――別々に無関係に測定できる――から、同じ土俵には上がれない、堅と白の関係である。無関係の尺度を比べるためには、どちらにも関係する第三の尺度で比べる以外の手はない。この比較表現で、wiseの比較級wiserを使わずに第三の尺度moreを使っている点が本稿の話を進める際に非常に重要である。ただし、wiserを使う比較構文もある[1]。結果的に、この例文には三つのスケール(wise,
clever, more)が存在する。
この議論から、賢さ、頭の良さ、moreは次の性質を持っていなければならないと結論できる。
(一)賢さスケールと頭の良さスケールは独立であり、互いに比較はできない。
(二)moreは賢さスケールと頭の良さスケールのどちらをも反映するスケールである。
以下で、比較を直接測るスケール(more)を比較スケールと呼ぶ。
性質(一)と(二)はユークリッド空間の内積できれいに説明できる。図1には三つのベクトルが描かれている。
● 賢さベクトルX(Xの長さが賢さの測定値)
● 頭の良さベクトルY(Yの長さが頭の良さの測定値)
● 比較ベクトルZ(比較スケールmoreを表すベクトル)
ベクトルXとYが直交していることは賢さと頭の良さが独立で無関係な概念であることに対応している。つまり、独立な概念をベクトルで表すと、これらは直交し、その内積はゼロである。比較ベクトルZはXとYのどちらとも関係がなければならず、XとZの内積、YとZの内積はどちらもゼロではない。まとめると、XとYが直交すると内積はゼロでこれらは独立で無関係、ZとX(またはY)が直交していないと内積がゼロでなく、これらは何かしらの関係がある。これで、上記の性質(一)と(二)を満足するベクトルX、Y、Zが得られた。比較の対象の測定値を表すベクトルXとYを要素ベクトルと呼ぶことにする。
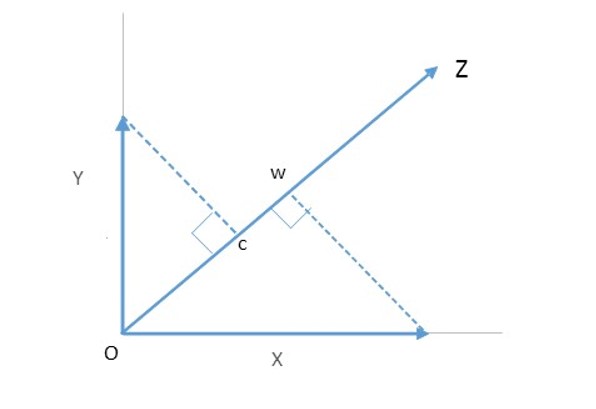
図1 二次元ユークリッド空間における要素ベクトルXとYと比較ベクトルZ
次に、比較の論理を一般化するために、写像(map)を定義しよう。
● XのZへの写像をベクトルX’とする(Xの頂点からZへ下した垂線wを頂点とするベクトルOw)
● YのZへの写像をベクトルY’とする(Yの頂点からZへ下した垂線cを頂点とするベクトルOc)
比較ベクトルZへの写像X’とY’の長さを比べれば、彼の賢さXと頭の良さYを比較できる。図1は「彼は頭が良いというより賢い」を表している。Oxford辞典によれば、mapはある物事がどのように構成されているかに関する情報を取得することであるから、図1の写像は物事の性質を表す要素ベクトルXとYに関する情報を比較ベクトルZの方向に限定して取り出すことに対応する。もちろん、人は写像を使って物事を評価・比較しているわけではないが、似たような思考を無意識に行っていると考えても良いだろう。
定数項とベクトルの積とベクトルの和(と差)を定義した空間がベクトル空間であり、ベクトル空間に内積を与えた空間がユークリッド空間である。ゆえに、図1の比較はユークリッド空間における比較である。なお、ゴルフボール(G)と雹(H)の比較はスケールが一つ(bigger)であるから、前者と後者の大きさを表すベクトルGとHと比較ベクトルZはどれもX軸(bigを表す軸)上にある。つまり、G=G’であり、H=H’である。この場合は、一次元ユークリッド空間での比較となる。賢さと頭の良さの比較は、図1にあるように二次元ユークリッド空間での比較である。
以上で、比較の数学的解釈は完了した。数学用語は別として、考え方は実に単純である。しかし、この定式化が多く――あらゆるとは言わないまでも――比較表現に適用できなければ、その実質的な価値はない。そこで、応用として、「ブラックチョコレート(B)とホワイトチョコレート(W)のどちらが好きか」という比較を考察しよう。評価者(私)がBを好むならば、その英語は次のように書ける。
I like this black chocolate more than that white chocolate. ―私は此方のブラックチョコレートの方が彼方のホワイトチョコレートよりも好きだ。
対象はBとW、スケールがmore、関係はthanである。単純な英語であるが、moreが何を象徴しているかが次の問題である。
チョコレートの好みを決定するための要因――つまり、スケール――は沢山考えられるが、ここでは甘さ、堅さ(パリパリ感)、色、口の中での溶け方を取りあげる。これら四つのスケールは独立であるから、これらは互いに直交する四次元ユークリッド空間の要素ベクトルであり、比較ベクトルZはこの四次元空間内に存在すると、これまでの議論から推定できる。先ずBについて、四つのスケール(甘さ、堅さ(パリパリ感)、色、口の中での溶け方)についてそれぞれ採点し、四つの要素ベクトルを構築する。それぞれの要素ベクトルを比較ベクトルZに写像し、写像したすべての要素ベクトルの和をBの総合評価ベクトルとする。同様に、Wについても同じ比較ベクトルZへの写像を実行し総合評価ベクトルを得る。これら二つの総合評価ベクトルを比べれば、この比較は成立する。同一直線上――Z上――のベクトルを比べることが同じ尺度で測った公平な比較を意味する。
比較対象の評価は評価者の嗜好や主義を反映するものであるから、評価ベクトルは、これを反映するように、要素ベクトルの作る空間内に任意に設定できるが、二つの対象の比較は必ず同一の比較ベクトルを使わなくてはならない。若しチョコレートの評価者が彼の判断の根拠を尋ねられたら、次のように説明するかもしれない。「確かにWの甘さ(要素ベクトル)は際立っているのだけれど、私の好み(比較ベクトル)は堅さとか色(要素ベクトル)に偏っている」。チョコレートの比較は文章にすれば何の変哲もないが、多次元ユークリッド空間での写像という背景がある。人は比較対象の個々の性質を別々に評価(要素ベクトル)し、次に、己の評価基準(比較ベクトル)に従って、それらを総合的に判定(写像)する。
一般に、比較スケールmoreの内訳は、ゴルフボールの例で示した単一スケールbiggerほど単純ではない。賢さと頭の良さの例は二次元ユークリッド空間での比較であり、チョコレートの例は四次元の比較である。なお、クジラの公式の比較スケールもmoreであるが、一次元の比較である[1]。K.
IshiguroのThe remains of the dayの中の文章「その家は幅より、高さがあった(拙訳)」は二次元の比較である[1]。
ニュートン物理学はユークリッド空間、量子力学はヒルベルト空間、ランダム過程を扱う確率過程論はガウス空間で定義される。いずれも、その根底はユークリッド空間にある。普段何気なく使っている言葉の裏に潜んでいる数学理論は、自然の全(また)き法則、つまり宇宙の真理とも言える古典・現代物理学、確率過程論と共通の基盤に立脚している。
人の思考の論理性が比較の言葉に自然に現われていることをこれまで考察してきたが、それがどこから来るのかは科学的な手がかり無しの神秘である。中原中也は、詩人は言葉を口にするまえ(名辞以前)に、躰に沁みた何かについて芸術の本質的な作業をすると述べた[3]。彼は、名辞以前とは人が創造した言葉では直截に表現できない真理や摂理が存在する神の領域、そして、それは天与の資でもあると考えたようだ。詩の心と同様に、人の思考の論理性も名辞以前に由来すると思える。ならば、数学者が「発明」した論理体系であるユークリッド空間は、ヒトの頭脳に生まれながらにして織り込まれていて、数学者が意識の撚糸にしなやかな探り針を這わせて辿り着いた「発見」かもしれない。
(付録)
会話の主要な目的は聞き手が知らない未知情報を話し手から伝えることであるから、数値だけを比較する順序集合――たとえば、整数の集合――やC++の構文には存在しない特有の規則がある。最初の例文では、ある時にある処で降った雹(H)の大きさ(未知情報)を聞き手に伝えるために、誰でもが知っているゴルフボール(G)の大きさを基準(既知情報)としている。未知情報をthanの前、既知情報をthanの後に置いて、早く伝えたい情報を先行させる。既知情報は比較の基準であり、ゴルフボールに限らず、ピンポン玉でもよいから、情報伝達の重要性の点で後に来るのである。
賢さと頭の良さの例を「我々は彼を頭が良いと考えているのだが、本当のところは賢いのだ」と意訳すれば、我々に共通な知識(既知情報)は頭の良さで、新しい主張(未知情報)が賢さと解釈できる。
次の例文から、今述べた情報伝達の規則を確認できる。
I felt more dead than alive.―生きた心地がしなかった。
比較の対象はdeadとalive、判定基準はthanである。moreは話し手自身の感覚を表す比較スケールであり、その測定値はaliveよりもdeadの方が大きい。話し手も聞き手も生きていて死んではいないから、当然、彼らが共有できる既知情報はaliveである。例文を丸暗記するとdeadとaliveの順序で迷うかもしれないが、情報伝達の規則を知っていれば、その心配はない。死は未知と悟れば、生(しょう)に迷いはない。
参考文献
[1] 拙著「英語の比較構文に潜むユークリッド空間」
[2] 鈴木大拙、禅とは何か、角川ソフィア文庫
[3] 中原中也、在りし日の歌・芸術論覚え書、学研の日本文学
令和二年五月二十一日