II．ユークリッド空間における比較
前章Iでは、比較の原理（要素、尺度、関係）に基づいて、
The hailstones were bigger than golf balls.―その雹の粒はゴルフボールより大きかった。
を、話し手が尺度biggerをもって雹の粒の大きさとゴルフボールの大きさの関係（大なり）を述べていると解釈した。では、Kazuo IshiguroのThe remains of the dayの中の文章
it (the house) was taller than it was broad ―その家は幅より、高さがあった（拙訳）。
は、尺度tallerをもって家の「高さ」と何の「高さ」を比べているのか？本章IIはこの問題を取りあげる。英語の比較構文はユークリッド空間の写像として統一的に解釈できることも示す。入門編は「林 譲→エッセイ集→堅白同異ーー英語の比較構文」。
II-1．比較構文の形式
形容詞の比較級を用いる比較の構文は、
X ＋ スケール ＋ than ＋ Y （式1）
である。XとYが比較の要素であり、スケールが比較級形容詞であり、thanがオペレータである。thanは＞に固定する（以下参照）。前章Iで、比較の原理が英語構文においても成り立つことが証明できたので、本章IIでは、式1に基づいて比較の文を解剖する。
II-2．一次元ユークリッド空間
本項の目的は要素XとYをベクトルとして定義し、比較構文を定式化することにある。定数項とベクトルの積とベクトルの和（と差）を定義した空間がベクトル空間であり、ベクトル空間に内積を与えた空間がユークリッド空間である。
式1を冒頭の例「その雹の粒はゴルフボールより大きかった」に適用する。
X = The hailstones were ……
Y = Golf balls were ……
スケール = bigger
be動詞の補語を不問（……）としている理由は雹とゴルフボールは同じスケールではかることと、比較は相対的であり、どちらかが絶対的に大きいとは限らないことにある。上記のX、Yとスケールを式1に代入し、重複する語句を消去すれば、目的の式（再掲）
The hailstones were bigger than golf balls. ―その雹の粒はゴルフボールより大きかった。
が得られる。
比較構文に関するベクトルを次のように定義する。
● Xを、始点がゼロ（原点）で終点が要素Xに関する話し手のスケール（測定値）であるベクトルとする。ベクトルYを要素Yに関する同様のベクトルとする。ベクトルXおよびベクトルYを要素ベクトルと呼ぶ。
● X＝数値およびY＝数値と書いて、ベクトルの終点とする。
● 差ベクトルδを次のように定義する。
δ ＝（対象）－（基準）＝ X – Y （式2）
XとYは要素（名詞または命題）だけでなく、ベクトルとその長さも表すと定義する。Xは比較の対象を表す要素ベクトル、Yは比較の基準を表す要素ベクトルである。上の文章において、雹の粒の直径を5.0cm、ゴルフボールの直径を4.3cmと仮定すると、X＝5.0cmおよびY＝4.3cmである。Yが基準であるから、差ベクトルはδ＝0.7cmとなり、正の値をとる（δ＞0、正の方向を向く）。一般に、比較はあるスケールで二つの要素をはかって、その測定値を比べるのであるから、相対値δが重要である。
差ベクトルδの方向について考察する。雹の粒がゴルフボールより小さい場合、たとえば、X＝4.0cm、Y＝4.3cmとすれば、差ベクトルδ＝X－Yは負の値（δ＜0）をとる。この場合には、上の文章のスケールbiggerを対義語smallerに変更する。話し手は差δ＝X – Yが正の時はbiggerと言い、差が負の時はsmallerと言うのである。ユークリッド空間の用語を使うと、次のようになる。話し手の判断（要素ベクトルXとY）は同一直線上のベクトルであり、その差δ＝X – Yが正方向を向いたベクトルであれば（δ＞0）、X bigger than Yと書き、差が負のベクトルであれば（δ＜0）、対義語のスケールを使い、X smaller than Yと書く。
「大きさ」（長さ）が正の数に限定されているので、smallerは負の値をもって「より小さい」を表すと考える。「負の大きさ」を身近に感じられる例としては、偏差値に基づいた成績の評価がある。ある人の偏差値が平均（＝50）よりも大きければ、成績は良いと判断し、そうでなければ悪いと判断する。この「悪い」には負のイメージ、つまり（その人の偏差値）－（平均）が付随するだろう。
thanは話し手の判断で可能性が高い事項を左辺に置くというオペレータ（＞）と考える。集合論やプログラミング言語は＞と＜の両方のオペレータを採用しているが、本稿は式1の比較構文に＞だけを採用する。なぜならば、bigger thanを＞で表し、smaller thanを＜で表すと、共通項thanに適切な意味を与えることが難しいからである。thanは意味のない置き字ではない。やはり、次の解釈が妥当である。than（＞）は数値の大小を比べるオペレータではなく、bigger thanでは、「bigger」スケールではかった可能性はthan（＞）の左側の要素Xの方が右側の要素Yより高く、smaller thanでは、「smaller」スケールではかった可能性はthan（＞）の左側のXの方が右側のYより高い。英語構文は二つのオペレータを採用する代わりに、二方向性のスケール（ベクトル）を選択する。
「クジラの公式」は、
X = A whale is a fish.
Y = A horse is a fish.
スケール ＝ no more
を式1に代入し、重複した項を消去すれば（すこしの並べ替えもする）、
A whale is no more a fish than a horse is.―クジラが魚であることは、馬が魚であるほどの可能性しかない。
となる。moreを話し手のスケールとした一次元空間での比較である。比較の結果はδ＝X－Y≒0である。前項では、「クジラの公式」の説明に多くのスペースを割いたが、式1と式2を用いれば、もはやその必要はないだろう。解釈は「要素Xの可能性は要素Yの可能性ほどしかない」（δ＝X－Y≒0）である。
要素Xが雹の粒で要素Yがゴルフボールでも、Xが「クジラが魚である」でYが「馬が魚である」でも、比較形式（δ＝X－Y）は同じである。もちろん、判定のルールによって結果（δ＞0、δ＜0、δ≒0）は異なる。要素XとYの比較とは、XとYを個別に単一のスケールで判定（要素ベクトルXとY）し、対比（δ＝X－Y）し、その結果（δ＞0、δ＜0またはδ≒0）を比較構文に載せて聞き手に伝えることである。
II-3．二次元ユークリッド空間
本章の主題を扱うために、まずは、次の例文を式1に基づいて考察する。
He is more wise than clever. ―彼は頭がいいというより賢い。
この文章の要素とスケールは
X = He is wise.
Y = He is clever.
スケール = more
である。話し手は独自のスケールmoreをもって要素XとYを比べている。moreはwiseまたはcleverと同じではないが、どちらをも考慮しているスケールである（以下参照）。式1にX、Yとスケールを代入し、すこしの並べ替えをすれば、
He is more wise than he is clever.
が得られる。この文章を簡略化するには、二つの選択肢がある。第一番目の選択肢は重複している語句（he is）を省略することである。この操作により、本項II-3の冒頭の文章が得られる。この文章は式1から形式的に得られるが、次のように考えることもできる。wiseスケール（知識の量）とcleverスケール（物事の習得の速さ）は無関係であり互いに比べることはできないので、要素XとYを比べるためのスケールmoreを導入する。比較級wiserを使わない理由は、このスケールではcleverの程度を「測定」できないからである。そうではあっても、もう一つの選択肢はmore wiseをwiserと簡略化し
He is wiser than he is clever. ―彼は頭がいいというより賢い
とする。見かけ上の尺度はwiserであるが、実際の話し手の尺度はmoreと考えるべきだろう。冒頭のIshiguroの文章は第二の選択肢をとっている。こちらは便宜的な簡略化であるから、以下では正しいスケールが現れている第一の選択肢に対して議論を進める。
同様な比較構文の例を以下に示す。話し手の比較のスケールはどちらもmoreである。要素XとYは自明であるから省略する。
She was more frightened than hurt. ―彼女はけがよりもむしろ怖さのほうが大きかった。
His story made me more sad than angry. ―彼の話を聞いて、腹が立つより悲しくなった。
話し手が自分の物差し（more）で、thanの左側の方が右側よりもありそうだと述べている。
「賢さと頭のよさの比較」をもう一度、今回はユークリッド空間の概念を利用して分析する。話し手はwiseをスケールとして対象を測定し、その測定値をベクトルXとして構築する。cleverも同様にベクトルYを構築する。また、話し手はXとYの比較に用いるスケールmoreをベクトルZとして構築する。問題はベクトルX、YとZの関係を明らかにすることである（図1参照）。
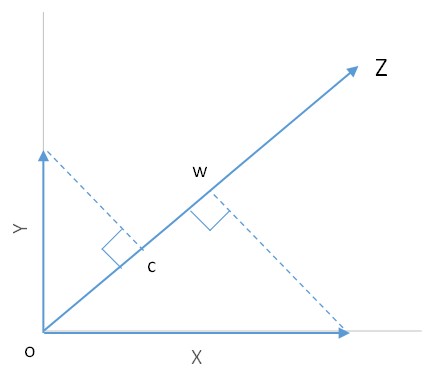図1 二次元ユークリッド空間における要素ベクトルX、要素ベクトルYと比較ベクトルZ
図1のベクトルを次のように定義する。
● XはX軸上にある要素ベクトルであり、YはY軸上にある要素ベクトルである。
● X－Y平面上にあるベクトルZを比較ベクトルと呼ぶ（大きさは1）。
● XのベクトルZへの写像をベクトルX’、YのベクトルZへの写像をベクトルY’とする。
● 差ベクトルδを次のように定義する。
δ ＝（対象）－（基準）＝ X’– Y’ （式3）
線分owはベクトルXとベクトルZとの内積である。ベクトルowはベクトルXのベクトルZへの写像（X’）であり、ベクトルZと同じ方向をもち、長さowのベクトルである。ベクトルYとベクトルZの内積が線分oc、ベクトルYのベクトルZへの写像がベクトルoc（Y’）である。写像はベクトルに重みを付けて（長さを変えて）、その方向を変える操作である。前項にある単純な比較では、X、YとZは同じ直線上にあったが、図1の考え方では、これらは同一直線上にはない。
比較に際して、話し手は対象の性質、wiseとclever、を別々に判断することから分析を始める。話し手が独自のスケールで対象のwiseの程度をはかった測定値が要素ベクトルXの長さである。同様に、ベクトルYはcleverの程度を表す。ベクトルXの大きさを知識の量、ベクトルYの大きさを物事の習得の速さとすれば、XとYは無関係であることが分かる。wiseとcleverが互いに比べられないことは、ベクトルXとYが直交している（内積がゼロである）ことに対応する。そこで、二つのベクトルXとYのどちらにも直交していない比較ベクトルZを設定する。
比較は、二つの要素をおなじスケールで測定しないと行えないので、この共通スケールをベクトルZとする。異なった（直交する）空間に存在するベクトルXとベクトルYを、同一空間Z（同一ベクトル）上に写像し、差ベクトルδ＝X’ – Y’（式3）を求めることにより、比較の演算ははじめて実行できる。ベクトルZ上への写像を実行した後では、Z上での比較は式2による比較と同じである。上の文章では、差ベクトルδ＝X’ – Y’はベクトルZの正方向を向いている（δ＞0）ので、話し手の判断は「彼は頭がいいというより賢い」となる（図1参照）。
別な方向を向いているため比べられないベクトルXとベクトルYを比べるためには、これらを同じ土俵上（ベクトルZ）で対峙させなければならない。その際、XとYの重要性（話し手が考える相対的な重要性）に従って、XとYに重みを付けて同じ土俵にあげるのである。要素間の相対的な重要性を重みとして担い、土俵に上がった要素がX’とY’である。XとYに重みを付けて土俵に上げる操作が写像である。XとYは要素ごとの判断であり、X’とY’は異なったスケールのどちらをも考慮した総合的な判断である。数学的には、写像が付ける重みは、比較ベクトルZの方向により一意に決定される。
単純な比較「雹の比較」では、bigを表すスケールをX軸とすれば、対象の要素ベクトルXと基準の要素ベクトルYと比較ベクトルZはすべてX軸上にある。「クジラの公式」も、話し手のスケールmoreをX軸とすれば、同様である。これらは一次元ユークリッド空間での比較である。二次元空間での比較では、ベクトルX、YとZは同じ平面上にあるが、同一直線上にはない（図1参照）。しかし、写像ベクトルX’とY’は同一直線上（Z）にある。つまり、要素ベクトルXとYが二次元空間を張っても、比較の判断（対比δ）は必ず一次元空間（単一のスケールZ）で行われる。「賢さと頭のよさの比較」だけではなく、「怖さとけがの比較」と「悲しさと立腹の比較」も同様に二次元ユークリッド空間での比較として定式化できることは言うまでもない。
前項で得た結論を二次元ユークリッド空間に拡張してもう一度述べる。要素XとYの比較とは、XとYをそれぞれに固有なスケールで判断（要素ベクトルXとY）し、それらを共通のスケールZの要素に変換（ベクトルZへの写像、X’ とY’）し、対比（δ＝X’ – Y’）し、その結果（δ＞0、δ＜0またはδ≒0）を比較構文に載せて聞き手に伝えることである。比較の手順としては、要素の選択→要素の測定→測定値の対比であり、二つの小石の重さを比べることと何ら変わるところはない。
話し手が「彼は頭がいいというより賢い」と主張したときに、他人が「それはどういう理由で？」と尋ねたとしよう。もし答えが曖昧ならば、「君、それは見解がバラバラだ。統一されていない。フェアーじゃないね」と言い返されたかもしれない。つまり、話し手が単一のスケールZで合理的に判断しなければ、聞き手は納得しないのである。
II-4．おわりに
二次元ユークリッド空間での比較を多次元空間に拡張することは容易である。そうでなければ、ユークリッド空間での比較の定式化は有意義とは言えない。例として、自動車を購入する場合、二つのモデルに対して、安全性、操作性、費用の三つのスケールで検討することを想像しよう。モデルの評価は三次元空間のベクトルX1＝（安全性の値、操作性の値、費用の値）とし、X2も同様とする。次に、自分の評価スケールをベクトルZとして三次元空間中に設定する。比較はX1とX2を評価ベクトルZへ写像し、写像したベクトルの差（δ＝X’ – Y’）をとり、どちらが自分の好みZにあっているかを検討すれば、完了する。
n個のモデルのm個のスケールによる比較は、m次元空間におけるn個のベクトルの評価ベクトルZへの写像である。つまり、n個のベクトルXi＝（スケール1の値、……、スケールmの値）（i = 1, ……, n）を評価ベクトルZへ写像することにより、n個のベクトルが得られるので、これらをZ上で対比する（δ＝Xi’ – Xj’）。考慮すべきスケール（プロパティ）の数がユークリッド空間の次元mであり、対象となる要素の数nだけのベクトルが構築される。ただし、比較はかならず一次元空間（ベクトルZ）で行われる。
小説を味わうときのポイントとして九の尺度をあげよう――人物描写、自然描写、心理描写、行動描写、形容詞と副詞の使い方、助詞の使い方、句読点、段落、主題の表現。比較の要素として十二の小説を列挙する。｛阿部一族、坊ちゃん、武蔵野、刺青、恩讐の彼方に、羅生門、伊豆の踊子、檸檬、風立ちぬ、天平の甍、お伽草子、金閣寺｝である。これで、九次元ユークリッド空間における十二の点（ベクトル）が構築された。自分の好みを勘案したベクトルZを設定すれば、文学作品ベクトルのZへの写像により、自分の好みの順序が決定できる。当然であるが、ユークリッド空間を意識して自分の好みを決定する人はいない。しかし、多くの人は無意識にではあっても、いくつかの独立な尺度をもって作品を別々に評価し、最終的には、これらの尺度を撚り合わせて作った自分独自の尺度によって、作品を総合的に評価するだろう。この思考プロセスは多次元ユークリッド空間における写像と極めて似ていないだろうか。
人が何気なく使っている言葉の中にユークリッド空間の概念が潜んでいるのならば、ヒトの脳にはユークリッド空間に対応する神経回路網が存在していても不思議ではない。この回路網はヒトが言語を習得したときにできあがったのかもしれない。すると、線形代数、ベクトル解析などが好きな人がベクトルに親近感をおぼえ、ベクトルは現実にあるものだと錯覚するのは無理もない話である。春のあけぼのに山ぎわから射してくる紫の光はまさにベクトルだと思い、夏の月夜の木の影を写像と思い……。
思考、経験、記憶などの精神作用の研究はたいへん興味深い。デカルトは神が創造した自然は感覚的に感知できるが、その理解はやはり神から与えられた理性（数学）によると主張した。これを裏付けるために、彼は「われ思う。故に我あり」として理性と感性を分離し、神の存在証明を行った。しかし、その後に表れたドイツ観念論も同様であるが、この哲学は実証性を欠いていた。十九世紀になると、経験主義と実証主義にもとづく自然科学が台頭したが、言うまでもなく、理性と経験の関係は自然科学の範疇にはなかった。フッサールは目で見ることなどの直接経験のなかに、数学や論理学の根本原理が含まれていると考えた。つまり、論理的思考は直接経験から「直観」によって抽出されるのである。彼はこの考え方を現象学とよんだ。西洋哲学は自然（存在するものの全体）を超自然的存在の観点から見るのであるが、仏教は人間は自然のなかにすっぽり取り込まれているとして、超自然的で絶対不変な真実は否定し、諸行無常と教える。そして、肉体と精神はべつべつにあるのではなく、同一であることを、身心一如という。
経験（言語）のなかに潜む論理（ユークリッド空間）とは、フッサールの現象学とも仏教の教えとも似ているかもしれない。しかし、門外漢の妄想はここまでにしよう。徳川家康のことばに「及ばざるは過ぎたるよりまされり」がある。
林 譲 平成30年6月23日
前章Iでは、比較の原理（要素、尺度、関係）に基づいて、
The hailstones were bigger than golf balls.―その雹の粒はゴルフボールより大きかった。
を、話し手が尺度biggerをもって雹の粒の大きさとゴルフボールの大きさの関係（大なり）を述べていると解釈した。では、Kazuo IshiguroのThe remains of the dayの中の文章
it (the house) was taller than it was broad ―その家は幅より、高さがあった（拙訳）。
は、尺度tallerをもって家の「高さ」と何の「高さ」を比べているのか？本章IIはこの問題を取りあげる。英語の比較構文はユークリッド空間の写像として統一的に解釈できることも示す。入門編は「林 譲→エッセイ集→堅白同異ーー英語の比較構文」。
II-1．比較構文の形式
形容詞の比較級を用いる比較の構文は、
X ＋ スケール ＋ than ＋ Y （式1）
である。XとYが比較の要素であり、スケールが比較級形容詞であり、thanがオペレータである。thanは＞に固定する（以下参照）。前章Iで、比較の原理が英語構文においても成り立つことが証明できたので、本章IIでは、式1に基づいて比較の文を解剖する。
II-2．一次元ユークリッド空間
本項の目的は要素XとYをベクトルとして定義し、比較構文を定式化することにある。定数項とベクトルの積とベクトルの和（と差）を定義した空間がベクトル空間であり、ベクトル空間に内積を与えた空間がユークリッド空間である。
式1を冒頭の例「その雹の粒はゴルフボールより大きかった」に適用する。
X = The hailstones were ……
Y = Golf balls were ……
スケール = bigger
be動詞の補語を不問（……）としている理由は雹とゴルフボールは同じスケールではかることと、比較は相対的であり、どちらかが絶対的に大きいとは限らないことにある。上記のX、Yとスケールを式1に代入し、重複する語句を消去すれば、目的の式（再掲）
The hailstones were bigger than golf balls. ―その雹の粒はゴルフボールより大きかった。
が得られる。
比較構文に関するベクトルを次のように定義する。
● Xを、始点がゼロ（原点）で終点が要素Xに関する話し手のスケール（測定値）であるベクトルとする。ベクトルYを要素Yに関する同様のベクトルとする。ベクトルXおよびベクトルYを要素ベクトルと呼ぶ。
● X＝数値およびY＝数値と書いて、ベクトルの終点とする。
● 差ベクトルδを次のように定義する。
δ ＝（対象）－（基準）＝ X – Y （式2）
XとYは要素（名詞または命題）だけでなく、ベクトルとその長さも表すと定義する。Xは比較の対象を表す要素ベクトル、Yは比較の基準を表す要素ベクトルである。上の文章において、雹の粒の直径を5.0cm、ゴルフボールの直径を4.3cmと仮定すると、X＝5.0cmおよびY＝4.3cmである。Yが基準であるから、差ベクトルはδ＝0.7cmとなり、正の値をとる（δ＞0、正の方向を向く）。一般に、比較はあるスケールで二つの要素をはかって、その測定値を比べるのであるから、相対値δが重要である。
差ベクトルδの方向について考察する。雹の粒がゴルフボールより小さい場合、たとえば、X＝4.0cm、Y＝4.3cmとすれば、差ベクトルδ＝X－Yは負の値（δ＜0）をとる。この場合には、上の文章のスケールbiggerを対義語smallerに変更する。話し手は差δ＝X – Yが正の時はbiggerと言い、差が負の時はsmallerと言うのである。ユークリッド空間の用語を使うと、次のようになる。話し手の判断（要素ベクトルXとY）は同一直線上のベクトルであり、その差δ＝X – Yが正方向を向いたベクトルであれば（δ＞0）、X bigger than Yと書き、差が負のベクトルであれば（δ＜0）、対義語のスケールを使い、X smaller than Yと書く。
「大きさ」（長さ）が正の数に限定されているので、smallerは負の値をもって「より小さい」を表すと考える。「負の大きさ」を身近に感じられる例としては、偏差値に基づいた成績の評価がある。ある人の偏差値が平均（＝50）よりも大きければ、成績は良いと判断し、そうでなければ悪いと判断する。この「悪い」には負のイメージ、つまり（その人の偏差値）－（平均）が付随するだろう。
thanは話し手の判断で可能性が高い事項を左辺に置くというオペレータ（＞）と考える。集合論やプログラミング言語は＞と＜の両方のオペレータを採用しているが、本稿は式1の比較構文に＞だけを採用する。なぜならば、bigger thanを＞で表し、smaller thanを＜で表すと、共通項thanに適切な意味を与えることが難しいからである。thanは意味のない置き字ではない。やはり、次の解釈が妥当である。than（＞）は数値の大小を比べるオペレータではなく、bigger thanでは、「bigger」スケールではかった可能性はthan（＞）の左側の要素Xの方が右側の要素Yより高く、smaller thanでは、「smaller」スケールではかった可能性はthan（＞）の左側のXの方が右側のYより高い。英語構文は二つのオペレータを採用する代わりに、二方向性のスケール（ベクトル）を選択する。
「クジラの公式」は、
X = A whale is a fish.
Y = A horse is a fish.
スケール ＝ no more
を式1に代入し、重複した項を消去すれば（すこしの並べ替えもする）、
A whale is no more a fish than a horse is.―クジラが魚であることは、馬が魚であるほどの可能性しかない。
となる。moreを話し手のスケールとした一次元空間での比較である。比較の結果はδ＝X－Y≒0である。前項では、「クジラの公式」の説明に多くのスペースを割いたが、式1と式2を用いれば、もはやその必要はないだろう。解釈は「要素Xの可能性は要素Yの可能性ほどしかない」（δ＝X－Y≒0）である。
要素Xが雹の粒で要素Yがゴルフボールでも、Xが「クジラが魚である」でYが「馬が魚である」でも、比較形式（δ＝X－Y）は同じである。もちろん、判定のルールによって結果（δ＞0、δ＜0、δ≒0）は異なる。要素XとYの比較とは、XとYを個別に単一のスケールで判定（要素ベクトルXとY）し、対比（δ＝X－Y）し、その結果（δ＞0、δ＜0またはδ≒0）を比較構文に載せて聞き手に伝えることである。
II-3．二次元ユークリッド空間
本章の主題を扱うために、まずは、次の例文を式1に基づいて考察する。
He is more wise than clever. ―彼は頭がいいというより賢い。
この文章の要素とスケールは
X = He is wise.
Y = He is clever.
スケール = more
である。話し手は独自のスケールmoreをもって要素XとYを比べている。moreはwiseまたはcleverと同じではないが、どちらをも考慮しているスケールである（以下参照）。式1にX、Yとスケールを代入し、すこしの並べ替えをすれば、
He is more wise than he is clever.
が得られる。この文章を簡略化するには、二つの選択肢がある。第一番目の選択肢は重複している語句（he is）を省略することである。この操作により、本項II-3の冒頭の文章が得られる。この文章は式1から形式的に得られるが、次のように考えることもできる。wiseスケール（知識の量）とcleverスケール（物事の習得の速さ）は無関係であり互いに比べることはできないので、要素XとYを比べるためのスケールmoreを導入する。比較級wiserを使わない理由は、このスケールではcleverの程度を「測定」できないからである。そうではあっても、もう一つの選択肢はmore wiseをwiserと簡略化し
He is wiser than he is clever. ―彼は頭がいいというより賢い
とする。見かけ上の尺度はwiserであるが、実際の話し手の尺度はmoreと考えるべきだろう。冒頭のIshiguroの文章は第二の選択肢をとっている。こちらは便宜的な簡略化であるから、以下では正しいスケールが現れている第一の選択肢に対して議論を進める。
同様な比較構文の例を以下に示す。話し手の比較のスケールはどちらもmoreである。要素XとYは自明であるから省略する。
She was more frightened than hurt. ―彼女はけがよりもむしろ怖さのほうが大きかった。
His story made me more sad than angry. ―彼の話を聞いて、腹が立つより悲しくなった。
話し手が自分の物差し（more）で、thanの左側の方が右側よりもありそうだと述べている。
「賢さと頭のよさの比較」をもう一度、今回はユークリッド空間の概念を利用して分析する。話し手はwiseをスケールとして対象を測定し、その測定値をベクトルXとして構築する。cleverも同様にベクトルYを構築する。また、話し手はXとYの比較に用いるスケールmoreをベクトルZとして構築する。問題はベクトルX、YとZの関係を明らかにすることである（図1参照）。
図1 二次元ユークリッド空間における要素ベクトルX、要素ベクトルYと比較ベクトルZ図1のベクトルを次のように定義する。
● XはX軸上にある要素ベクトルであり、YはY軸上にある要素ベクトルである。
● X－Y平面上にあるベクトルZを比較ベクトルと呼ぶ（大きさは1）。
● XのベクトルZへの写像をベクトルX’、YのベクトルZへの写像をベクトルY’とする。
● 差ベクトルδを次のように定義する。
δ ＝（対象）－（基準）＝ X’– Y’ （式3）
線分owはベクトルXとベクトルZとの内積である。ベクトルowはベクトルXのベクトルZへの写像（X’）であり、ベクトルZと同じ方向をもち、長さowのベクトルである。ベクトルYとベクトルZの内積が線分oc、ベクトルYのベクトルZへの写像がベクトルoc（Y’）である。写像はベクトルに重みを付けて（長さを変えて）、その方向を変える操作である。前項にある単純な比較では、X、YとZは同じ直線上にあったが、図1の考え方では、これらは同一直線上にはない。
比較に際して、話し手は対象の性質、wiseとclever、を別々に判断することから分析を始める。話し手が独自のスケールで対象のwiseの程度をはかった測定値が要素ベクトルXの長さである。同様に、ベクトルYはcleverの程度を表す。ベクトルXの大きさを知識の量、ベクトルYの大きさを物事の習得の速さとすれば、XとYは無関係であることが分かる。wiseとcleverが互いに比べられないことは、ベクトルXとYが直交している（内積がゼロである）ことに対応する。そこで、二つのベクトルXとYのどちらにも直交していない比較ベクトルZを設定する。
比較は、二つの要素をおなじスケールで測定しないと行えないので、この共通スケールをベクトルZとする。異なった（直交する）空間に存在するベクトルXとベクトルYを、同一空間Z（同一ベクトル）上に写像し、差ベクトルδ＝X’ – Y’（式3）を求めることにより、比較の演算ははじめて実行できる。ベクトルZ上への写像を実行した後では、Z上での比較は式2による比較と同じである。上の文章では、差ベクトルδ＝X’ – Y’はベクトルZの正方向を向いている（δ＞0）ので、話し手の判断は「彼は頭がいいというより賢い」となる（図1参照）。
別な方向を向いているため比べられないベクトルXとベクトルYを比べるためには、これらを同じ土俵上（ベクトルZ）で対峙させなければならない。その際、XとYの重要性（話し手が考える相対的な重要性）に従って、XとYに重みを付けて同じ土俵にあげるのである。要素間の相対的な重要性を重みとして担い、土俵に上がった要素がX’とY’である。XとYに重みを付けて土俵に上げる操作が写像である。XとYは要素ごとの判断であり、X’とY’は異なったスケールのどちらをも考慮した総合的な判断である。数学的には、写像が付ける重みは、比較ベクトルZの方向により一意に決定される。
単純な比較「雹の比較」では、bigを表すスケールをX軸とすれば、対象の要素ベクトルXと基準の要素ベクトルYと比較ベクトルZはすべてX軸上にある。「クジラの公式」も、話し手のスケールmoreをX軸とすれば、同様である。これらは一次元ユークリッド空間での比較である。二次元空間での比較では、ベクトルX、YとZは同じ平面上にあるが、同一直線上にはない（図1参照）。しかし、写像ベクトルX’とY’は同一直線上（Z）にある。つまり、要素ベクトルXとYが二次元空間を張っても、比較の判断（対比δ）は必ず一次元空間（単一のスケールZ）で行われる。「賢さと頭のよさの比較」だけではなく、「怖さとけがの比較」と「悲しさと立腹の比較」も同様に二次元ユークリッド空間での比較として定式化できることは言うまでもない。
前項で得た結論を二次元ユークリッド空間に拡張してもう一度述べる。要素XとYの比較とは、XとYをそれぞれに固有なスケールで判断（要素ベクトルXとY）し、それらを共通のスケールZの要素に変換（ベクトルZへの写像、X’ とY’）し、対比（δ＝X’ – Y’）し、その結果（δ＞0、δ＜0またはδ≒0）を比較構文に載せて聞き手に伝えることである。比較の手順としては、要素の選択→要素の測定→測定値の対比であり、二つの小石の重さを比べることと何ら変わるところはない。
話し手が「彼は頭がいいというより賢い」と主張したときに、他人が「それはどういう理由で？」と尋ねたとしよう。もし答えが曖昧ならば、「君、それは見解がバラバラだ。統一されていない。フェアーじゃないね」と言い返されたかもしれない。つまり、話し手が単一のスケールZで合理的に判断しなければ、聞き手は納得しないのである。
II-4．おわりに
二次元ユークリッド空間での比較を多次元空間に拡張することは容易である。そうでなければ、ユークリッド空間での比較の定式化は有意義とは言えない。例として、自動車を購入する場合、二つのモデルに対して、安全性、操作性、費用の三つのスケールで検討することを想像しよう。モデルの評価は三次元空間のベクトルX1＝（安全性の値、操作性の値、費用の値）とし、X2も同様とする。次に、自分の評価スケールをベクトルZとして三次元空間中に設定する。比較はX1とX2を評価ベクトルZへ写像し、写像したベクトルの差（δ＝X’ – Y’）をとり、どちらが自分の好みZにあっているかを検討すれば、完了する。
n個のモデルのm個のスケールによる比較は、m次元空間におけるn個のベクトルの評価ベクトルZへの写像である。つまり、n個のベクトルXi＝（スケール1の値、……、スケールmの値）（i = 1, ……, n）を評価ベクトルZへ写像することにより、n個のベクトルが得られるので、これらをZ上で対比する（δ＝Xi’ – Xj’）。考慮すべきスケール（プロパティ）の数がユークリッド空間の次元mであり、対象となる要素の数nだけのベクトルが構築される。ただし、比較はかならず一次元空間（ベクトルZ）で行われる。
小説を味わうときのポイントとして九の尺度をあげよう――人物描写、自然描写、心理描写、行動描写、形容詞と副詞の使い方、助詞の使い方、句読点、段落、主題の表現。比較の要素として十二の小説を列挙する。｛阿部一族、坊ちゃん、武蔵野、刺青、恩讐の彼方に、羅生門、伊豆の踊子、檸檬、風立ちぬ、天平の甍、お伽草子、金閣寺｝である。これで、九次元ユークリッド空間における十二の点（ベクトル）が構築された。自分の好みを勘案したベクトルZを設定すれば、文学作品ベクトルのZへの写像により、自分の好みの順序が決定できる。当然であるが、ユークリッド空間を意識して自分の好みを決定する人はいない。しかし、多くの人は無意識にではあっても、いくつかの独立な尺度をもって作品を別々に評価し、最終的には、これらの尺度を撚り合わせて作った自分独自の尺度によって、作品を総合的に評価するだろう。この思考プロセスは多次元ユークリッド空間における写像と極めて似ていないだろうか。
人が何気なく使っている言葉の中にユークリッド空間の概念が潜んでいるのならば、ヒトの脳にはユークリッド空間に対応する神経回路網が存在していても不思議ではない。この回路網はヒトが言語を習得したときにできあがったのかもしれない。すると、線形代数、ベクトル解析などが好きな人がベクトルに親近感をおぼえ、ベクトルは現実にあるものだと錯覚するのは無理もない話である。春のあけぼのに山ぎわから射してくる紫の光はまさにベクトルだと思い、夏の月夜の木の影を写像と思い……。
思考、経験、記憶などの精神作用の研究はたいへん興味深い。デカルトは神が創造した自然は感覚的に感知できるが、その理解はやはり神から与えられた理性（数学）によると主張した。これを裏付けるために、彼は「われ思う。故に我あり」として理性と感性を分離し、神の存在証明を行った。しかし、その後に表れたドイツ観念論も同様であるが、この哲学は実証性を欠いていた。十九世紀になると、経験主義と実証主義にもとづく自然科学が台頭したが、言うまでもなく、理性と経験の関係は自然科学の範疇にはなかった。フッサールは目で見ることなどの直接経験のなかに、数学や論理学の根本原理が含まれていると考えた。つまり、論理的思考は直接経験から「直観」によって抽出されるのである。彼はこの考え方を現象学とよんだ。西洋哲学は自然（存在するものの全体）を超自然的存在の観点から見るのであるが、仏教は人間は自然のなかにすっぽり取り込まれているとして、超自然的で絶対不変な真実は否定し、諸行無常と教える。そして、肉体と精神はべつべつにあるのではなく、同一であることを、身心一如という。
経験（言語）のなかに潜む論理（ユークリッド空間）とは、フッサールの現象学とも仏教の教えとも似ているかもしれない。しかし、門外漢の妄想はここまでにしよう。徳川家康のことばに「及ばざるは過ぎたるよりまされり」がある。
林 譲 平成30年6月23日